Certified robustness to adversarial examples with differential privacy

Certified robustness to adversarial examples with differential privacy

Columbia University: Mathias Lecuyer, Vaggelis Atlidakis, Roxana Geambasu, Daniel Hsu, and Suman Jana

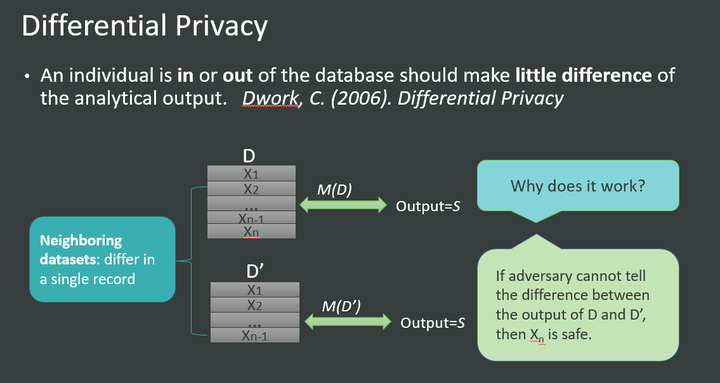
Definition of differential privacy: If you can find a way for an attacker to query 100 information in some way and the results obtained by querying the 99 information are the same, then the attacker cannot find the information of the 100th person.

How: add random noise, e.g. Laplace/Gaussian noise

Establishes the DP-robustness connection formally: treat the images as databases in DP parlance.

PixelDP DNN: includes a DP noise layer that randomizes the network’s computation to enforce DP bounds on how much the distribution over its predictions can change with small, norm-bounded changes in the input

At inference time, leverage these DP bounds to implement a certified robustness check for individual predictions. Passing the check for a given input guarantees that no perturbation exists up to a particular size that causes the network to change its prediction.(sound but incomplete)

Properties of DP:

• post-processing property: any computation applied to the output of an ($\epsilon,\delta$)-DP algorithm remains ($\epsilon,\delta$)-DP.
• expected output stability property: $\forall \alpha \in B_{p}(1) . \mathbb{E}(A(x)) \leq e^{\epsilon} \mathbb{E}(A(x+\alpha))+b \delta$

Robustness Condition: $\mathbb{E}\left(A_{k}\left(x^{\prime}\right)\right)>\max_{i: i \neq k} \mathbb{E}\left(A_{i}(x+\alpha)\right) \forall \alpha \in B_{p}(1)$, implies that the lower-bound of the expected score for label k is strictly higher than the upper-bound for the expected score for any other label.

Cannot compute the output expectation, resort to Monte Carlo method and develop an approximate version of the robustness certification. The failure probability of this robustness certification, 1−η, can be made arbitrarily small by increasing the number of invocations

Implementation:

• noise layer can be added in different places (input/after layer)
• multiple times with new draws of the noise layer, take average and compute η confidence interval
• integrates this confidence interval into the stability bound for the expectation of a DP computation
• apply Hoeffding’s inequality: $\hat{\mathbb{E}}^{l b}(A(x)) \triangleq \hat{\mathbb{E}}(A(x))-\sqrt{\frac{1}{2 n} \ln \left(\frac{2 k}{1-\eta}\right)} \leq \mathbb{E}(A(x)) \leq \hat{\mathbb{E}}(A(x))+\sqrt{\frac{1}{2 n} \ln \left(\frac{2 k}{1-\eta}\right)} \triangleq \hat{\mathbb{E}}^{u b}(A(x))$
• ImageNet, pre-trained Inceptionn-v3 (noise in auto-encoder)

Generalized Robustness Condition:

$\hat{\mathbb{E}}^{l b}\left(A_{k}(x)\right)>e^{2 \epsilon} \max_{i: i \neq k} \hat{\mathbb{E}}^{u b}\left(A_{i}(x)\right)+\left(1+e^{\epsilon}\right) \delta$

PixelDP not only can be used to certificates as binary with respect to a fixed attack bound L: meet or do not meet a robustness check for L, it also allows for a more nuanced certificate, which gives the maximum attack size $L_{max}$.

Code: https://github.com/columbia/pixeldp

---

• Previous
  Paper of Randomized smoothing
• Next
  Certified Adversarial Robustness via Randomized Smoothing

---