Certified Adversarial Robustness via Randomized Smoothing

Certified Adversarial Robustness via Randomized Smoothing

CMU: Jeremy Cohen, Elan Rosenfeld, J. Zico Kolter

Prove a tight robustness guarantee in $l_2$ norm for smoothing with Gaussian noise.

workaround: look for robust classifiers that are not neural networks

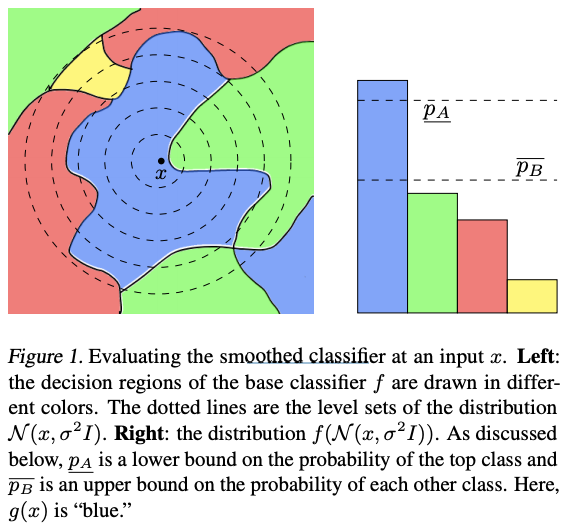
Randomized smoothing: can transform any arbitrary base classifier $f$ into a new “smoothed classifier” g that is certifiably robust in $l_2$ norm. For any input $x$, the smoothed classifier’s prediction $g(x)$ is defined to be the class which $f$ is most likely to classify the random variable $N(x, \sigma^2I)$ as. $g(x)$ returns the most probable prediction by $f$ of random Gaussian corruptions of $x$.

The smoothed classifier $g$ will also possess a desirable property that the base classifier may lack: one can verify that $g$’s prediction is constant within an l2 ball around any input $x$, simply by estimating the probabilities with which $f$ classifies $N(x, \sigma^2I)$ as each class.

The higher the probability with which f classifies $N(x, \sigma^2I)$ as the most probable class, the larger the $l_2$ radius around $x$ in which $g$ provably returns that class.

This paper proves the first tight robustness guarantee for randomized smoothing, and suspect that as-yet-unknown noise distributions might induce robustness to other perturbation sets such as general $l_p$ norm balls.

Drawback of randomized smoothing: it is not possible to exactly compute the probabilities with which $f$ classifies $N(x, \sigma^2I)$ as each class, so it is not possible to evaluate $g$’s predition for any $x$, or to exactly compute the radius for safety. (resorted by Monte Carlo algorithms)

Advantage of randomized smoothing: no assumptions about the base classifier’s architecture; scale to large networks

Conservative certification: sound but incomplete, more scalable

$g(x)$ returns the class $c$ whose pre-image {$x’ \in R: f(x’)=c$} has the largest probability measure under the distribution $N(x, \sigma^2I)$; $\sigma$ is a hyperparameter controlling a robustness/accuracy tradeoff.

Robustness guarantee:

$R=\frac{\sigma}{2}\left(\Phi^{-1}\left(\underline{p_{A}}\right)-\Phi^{-1}(\overline{p_{B}})\right)$

Binary case:

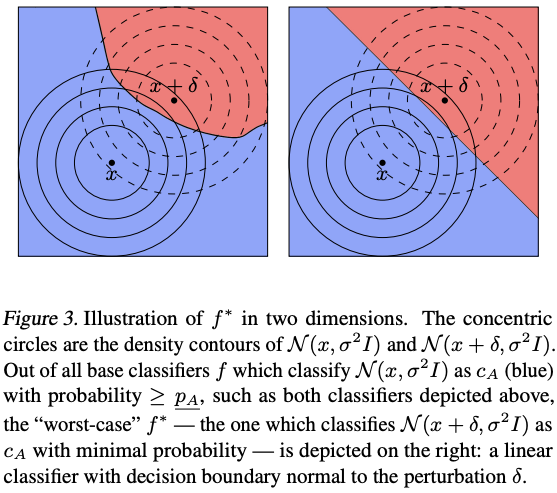
Large R may imply that:

• large $\sigma$
• the probability of the top class $c_A$ is high
• the probability of each other class is low
• R –> $\infty$: $\underline{p_{A}}$ –> 1, $\overline{p_{B}}$ –> 0

Assume $\underline{p_{A}}+\overline{p_{B}}\le 1$, for any perturbation $||\delta|| > R $, then there exists an adversarial example, i.e. $g(x+\delta) \ne c_A$. The set of perturbations to which a Gaussian-smoothed classifier is provably robust is exactly an $l_2$ ball.

Although he certified radius does not depend explicitly on the data dimension $d$, images in higher resolution can tolerate higher levels σ of isotropic Gaussian noise before their class-distinguishing content gets destroyed. In high resolution, smoothing can be performed with a larger $\sigma$, leading to larger certified radii.

Implementation:

• draws $n$ samples of $f(x + \epsilon)$ by running $n$ noise-corrupted copies of $x$ through the base classifier.
• predict or calibrate the abstention threshold
• CERTIFICATION: To get $f(x + \epsilon)$, $\underline{p_{A}}$ and $\overline{p_{B}}$ at the same time, use a small number of samples from all $f(x + \epsilon)$ and take a guess at $c_A$, then use a small number of samples to estimate $\underline{p_{A}}$ and $\overline{p_{B}}$ ($1-\underline{p_{A}}$).
• LOWERCONFBOUND: return a one-sided $(1 − \alpha)$ lower confidence interval for the Binomial parameter $p$.

Certifying large radii requires many samples.

Training

• In high dimension, the Gaussian distribution $N(x, \sigma^2I)$ places almost no mass near its mode x. Large $\sigma$ leads to the distribution of natural images has a disjoint support from that with $N(x, \sigma^2I)$.
• Follow Lecuyer et al. (2019), with Gaussian data augmentation
• suspect that there may be room to improve upon this training scheme perhaps by training the base classifier so as to maximize the smoothed classifier’s certified accuracy at some tunable radius.

Code: https://github.com/locuslab/smoothing

---

• Previous
  Certified robustness to adversarial examples with differential privacy
• Next
  Provably Robust Deep Learning via Adversarially Trained Smoothed Classifiers

---