https://arxiv.org/abs/1809.03368
Introduction
This paper is proposed by Jorn W.T. Peters and Max Welling in 2019 on ICLR 2019 (rejected). This blog will review the paper and reproduce some experiments. [code]
The compression of deep neural networks is a promising direction due to its vast memory requirement and low computational efficiency. And these drawbacks would seriously hinder its applications on mobile devices. Therefore, Binarized Neural Networks was proposed to improve the efficiency of deep neural networks and use in these limited environments with a lower memory and higher power efficiency. These is achieved by reducing the bit-width of both weights and activations in either training processes or post-training mechanisms.
In this project, a probabilistic binary neural network has been proposed to achieve a better performance than common binarized neural networks. In this approach, a closed forward propagation can be obtained by randomly binarizing both input and weights, and the output of the pre-activation can be approximated with a factorized Normal distribution. Then, stochastic versions of Batch Normalization is used for the propagation of the pre-activatoins throughout a single layer. Finally, the binary activations can be sampled with the concrete distribution during training, the input for subsequent layers matches the test input closely. This approach can be used to realize online training and further improve the computational efficiency.
Binarized neural networks
Binarized Neural Networks is proposed on [1]. The paper introduced a method to train neural networks with binary weights and activation parameters, aiming to achieve a low memory and power efficiency for small scale devices such as mobile phone.
The deterministic binarization process is introduced, it uses $sign$ function to convert real-valued variables to +1 and -1 during training. Though the equation below, binarized variables of $x$ can be obtained:
\begin{equation}
b_{det}(x) = {\rm Sign}(x) =
\begin{cases}
+1& \text{if x $\geq$ 0}\
-1& \text{Otherwise}
\end{cases}
\end{equation}
Although BNN uses binarized weights and activation parameters, the gradient can not be saved as binarized value since the gradient is small valued variables and normal distributed noise is contained in the gradient, it provides a method of regularization to improve generalization performance. The method of training BNN can be considered as a variant of dropout layer, instead of setting activation to zero randomly, BNN binarizes activation parameters.
PROBABILISTIC BINARY NEURAL NETWORK
This section describes our main reproduction work for probabilistic binary neural network (PBNet)[3]. The probabilistic setting and the approximation for the pre-activation of the network would be described. Unlike common binarized neural networks, a random binary distribution over the weights of the network would be generated first as the inputs coming in. Then, it can be slightly reparameterized with the Bernoulli distribution: \begin{equation} a \sim {\rm Binary}(\theta) \Longleftrightarrow \frac{a+1}{2} \sim {\rm Bernoulli}(\frac{\theta+1}{2}) \end{equation} Let $w\sim {\rm Binary}(\theta)$ and $h\sim {\rm Binary}(\phi)$ as two random binary variables, as such the inner product obtained by the element-wise multiplication of the random variables weight $w$ and activation $h$ for a previous layer will be a translated and scaled Poisson binomial distribution: \begin{equation} \frac{w \cdot h+D}{2} = {\rm PolBin}(2[\theta \odot \phi]-1) \end{equation} Where D is the unit matrix with the dimensionality of $h$ and $w$, $\odot$ is the element-wise multiplication. For the computational convenience, this Poisson binomial distributions can be well approximated by a Normal distribution [4] according to Lyapunov Central Limit Theorem (CLT). when the input is the output of previous layer, the approximation the pre-activation can be represented as: \begin{equation} a = w \cdot h \sim \mathcal{N}(\sum^D_{d=1}\theta_d\phi_d, D-\sum^D_{d=1}\theta_d^2\phi_d^2) \end{equation} This will obtain a close approximation to the pre-activation distribution, which can be propagated through the layer and/or network. However, for the real input value of the first layer $h$, whose distribution is not binary, hence the approximation of the pre-activation can be shown as: \begin{equation} a = w \cdot h \sim \mathcal{N}(\sum^D_{d=1}\theta_dh_d, \sum^D_{d=1}\theta_d^2h_d^2) \end{equation}
Stochastic Binary Activation
For the Stochastic Binary Activation process, since the pre-activations in this project are random variables, a deterministic binarization function can be used to implement it: \begin{equation} h_i = b_{det}(a_i) \sim {\rm Binary}(q_i),\quad q_i= 1- \Phi(0|\mu,\sigma^2) \end{equation} where $\Phi(0|\mu,\sigma^2)$ is the CDF of $N(\mu, \sigma^2)$. Surprisingly, the Cumulative Distribution Function of Gaussian can be employed as the probability of pre-activation. However, we found that this binary implementation to obtain $h$ is redundant in practical, as the distribution $p$ already can be propagated thought the network.
Stochastic Batch Normalization
[3] introduces a Stochastic version of Batch Normalization, whose implementation are focus on the distribution of the input (pre-activation) rather than do the normalization for the input value. Hence the population mean and variance can not be applied directly, we calculate the expected mean and variance under the pre-activation distribution. This makes mean $\mathbb{E}[m]$ and variance $\mathbb{E}[v]$ of the distribution of pre-activation after batch normalization can still be approximately zero and unit respectively for the transformation to deterministic BNN. Then, the Gaussian distributions for the pre-activations after Batch Normalization can be obtained as: \begin{equation} \hat{a_i} = \frac{a_i - \mathbb{E}[m]}{\sqrt{\mathbb[v]+\epsilon}}\gamma + \beta \Longrightarrow \hat{a_i} \sim \mathcal{N}(\frac{\mu_i - \mathbb{E}[m]}{\sqrt{\mathbb{E}[v]+\epsilon}}\gamma + \beta, \frac{\gamma^2}{\mathbb{E}[v]+\epsilon}\sigma_i^2) \end{equation}
The updating implementation for the scaling factor $\gamma$ translation parameter $\beta$ has not given in his paper. Therefore, in our experiment, we assume them as the unlearned affine transform, i.e. without changing the value of $\gamma$ and $\beta$ during training.
Stochastic Max Pooling
Besides the Stochastic Batch Normalization, the Stochastic version of Max Pooling is introduced in PBNet. In short, it uses the local reparametrization trick [2] $s = \mu+\sigma\odot n, n\sim \mathcal{N}(0,1)$ to sample one of the input random variables in every spatial region according to the probability of that variable being greater than all other variables. Then the obtained indices of the sample is used for corresponding selection of the distribution (mean and variance). However, we found out that this implementation is resource consuming which drops the speed a lot. Alternatively, we implemented the max pooling on mean and variance of pre-activation, respectively, which speeds up the training process and achieves good performance. The experimental result containing operations described above is reported below.
Experiment
Following the description in [3], we build and reproduce the neural network on the MNIST dataset using the structure below: \begin{equation*} 32C3 - MP2 - 64C3 - MP2 - 512FC - SM10 \end{equation*} where $X$C3 denotes a binary convolutional layer with 3 $\times$ 3 filters and X output channels, $Y$FC denotes a fully connected layer with $Y$ output neurons, SM10 denotes a Softmax layer (achieved by Pytorch automatically) with 10 outputs, and MP2 denotes 2 $\times$ 2 (stochastic) max pooling with stride 2. The loss function is defined using cross entropy, meanwhile the output of the final layer is replaced by the mean of Gaussian approximation. During training, all binary weight parameters are clipped between in [-0.9, 0.9].
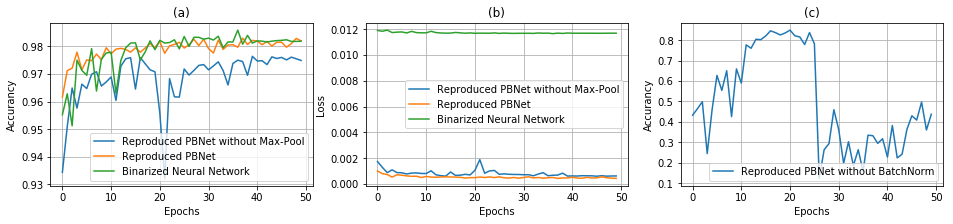
Since the source code of the PBNet is not released, we conducted the experiment on the Binarized Neural Networks [1] using the same operation sequence for comparison. The experimental results are shown in Fig. 1(a)(b). The reproduced PBNet demonstrates a similar performance of BNN but converges more smoothly. Although the reproduced PBNet achieves smaller mean loss, the highest accuracy is still obtained using BNN (98.6%) if compared with reproduced PBNet (98.3%).
In addition, we try to prove the feasibility of stochastic batch normalization and max pooling, hence an ablation study was performed on both operators.
we removed all batch normalization layers and remained others to training the network.
We observed that without batch normalization, the accuracy on the test set illustrates a huge fluctuation, approximately from 12% to 90% on our observation, which can be seen in Fig. 1(c).
In terms of max pooling, the performance of reproduced PBNet without max pooling drops slightly about 1%.
The results described above prove the importance of stochastic batch normalization and stochastic max pooling.
\section{Discussion} As it is discussed, the aim of BinaryNet is to save more memory and achieve less processing power in order to bring neural network processing to power-consumption critical mobile devices. in the paper, a optimization method is proposed, binary addition operation for BinaryNet can be achieved by using XOR operation, which is easier to implement in hardware layer and achieve a 7 times faster performance. However, the author of PBNet has not proposed a method to improve computing efficiency in mobile devices. Time performance of the proposed network is not mentioned in the original paper. Additionally, PBNet proposed in the paper is not proven having advantages for large datasets such as ImageNet. Two convolution operations are involved for solving mean and variance during the training, this will cause a longer wall clock time if the hardware does not permit parallelization .
Jorn et al. missed some significant information in their paper, which increases the difficulty of this reproduction work, e.g. the binary distribution of weight $w$ is obtained by using $\theta = \tanh(w)$, thus the distribution can be propagated thought layers; the stochastic batch normalization introduced in the paper misses the practical implementation for two parameters, i.e. $\gamma$ and $\beta$. As one of the reviewers of ICLR described [3], generally the paper of PBNet was written in poor quality and did not present enough details.
Nevertheless, there are still several limitations of our work, some details in Jorn’s work have not been reproduced, e.g. sampling the activation for ensemble predictions, which can be used for enhancing performance and uncertainty estimates.
Conclusion
In conclusion, a Probabilistic Binary Neural Network is reproduced bases on Jorn’s paper. Proposed features such as the embracement of stochasticity in the training process, stochastic versions of Batch Normalization and sampling in binary activations are implemented. Our model is evaluated and compared with Binarized Neural Networks, similar results have been obtained. Result and limitations of Probabilistic Binary Neural Networks is discussed.
Code for experiment
https://github.com/COMP6248-Reproducability-Challenge/Reproduction-of-Probabilistic-binary-neural-networks
References
[1] Itay Hubara, Matthieu Courbariaux, Daniel Soudry, Ran El-Yaniv, and Yoshua Bengio. Binarized neural networks. In Advances in neural information processing systems, pp. 4107–4115, 2016.
[2] Diederik P Kingma and Max Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.
[3] Jorn W.T. Peters, Tim Genewein, and Max Welling. Probabilistic binary neural networks, 2019. URL https://openreview.net/forum?id=B1fysiAqK7.
[4] Sida Wang and Christopher Manning. Fast dropout training. In international conference on machine learn- ing, pp. 118–126, 2013.