Semi-Supervised Classification with Graph Convolutional Networks

https://arxiv.org/abs/1609.02907

Introduction

This paper is proposed by Kipf, Thomas N., and Max Welling. in 2017 on ICLR.

This blog will review the paper and reproduce some experiments. [code]

Problem：Classification nodes(e.g. documents) in a graph(e.g. citation network)

So not all nodes have lables -> semi-supervised.

Previous work is based on the assumption that connected nodes in the graph are likely to share the same label: \begin{equation} \mathcal{L} = \mathcal{L}_{0} +\lambda \mathcal{L}_{reg}, \ with \ \mathcal{L}_{reg} = \sum_{i,j} A_{i,j}||f(X_i)-f(X_j)||^2 = f(X)^T\Delta f(X) \end{equation}

$\mathcal{L}_{0}$: supervised loss
$\lambda$: a weighing factor
$X$: matrix of node feature
$\Delta = D-A$: unnormalized graph Laplacian of an undirected graph $G=(V,\varepsilon)$ -> (node,edge)
$A$: adjacncy matrix
$D$: degree matrix, $D_{i,i}=\sum_{j}A_{i,j}$

This assumption, however, might restrict modeling capacity, as graph edges need not necessarily encode node similarity, but could contain additional information.

This paper directly encodes the graph structure using the neural network model $f(X,A)$ and trains on the the above targe $\mathcal{L}_{0}$, so this avoids explicit graph-based regularization in the loss function. $f(\cdot)$ on $A$ allows the model to distribute gradient information from $\mathcal{L}_{0}$, so the representation of nodes with and without labels can be learned.

Convolution on Graph

Following layer-wise propagation rule for a multi-layer Graph Convolutional Network: \begin{equation} H^{(l+1)} = \sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}) \end{equation}

$\tilde{A} = A+I$: the adjacency matrix of the undirected graph $G$ with added self-connections.
$\tilde{D}_{i,i}=\sum_{j}\tilde{A}_{i,j}$
$W$: a layer-specific trainable wight matrix.
$\sigma(\cdot)$: activation function, $e.g.$ ${\rm ReLU}(\cdot) = max(0,\cdot)$
$H^{(l)}$: the matrix of activations in the $l$th layer, $H^{(0)}=X$

This form of propagation rule can be motivated via a first-order approximation of localized spectral filters on graphs.

Spectral Graph Convolution

Define the Spectral Graph Convolution as the multiplication of a signal $x\in \Re^N$ with a filter $g_{\theta} = {\rm diag}(\theta),\theta\in \Re^N$ in the frequency domain, $i.e.$ Fourier Transform: \begin{equation} g_{\theta}\star x = Ug_{\theta}U^Tx \end{equation}

$U$: the matrix of eigenvectors of the symmetric normalized graph Laplacian $L = I - D^{-\frac{1}{2}}AD^{-\frac{1}{2}} = D^{-\frac{1}{2}}\Delta D^{-\frac{1}{2}} = U\Lambda U^T$
$\Lambda$: a diagonal matrix of its eigenvalues
$U^Tx$: the graph Fourier transform of $x$
so $g_{\theta}$ acts as a function of the eigenvalues of $L$, $i.e.$ $g_{\theta}(\Lambda)$.

However, the time complexity is $\mathcal{O}(N^2)$. This can be circumvented and $g_{\theta}(\Lambda)$ can be well-approximated by a truncated expansion with respect to Chebyshev polynomials $T_k(x)$ up to $K$th order[2]: \begin{equation} g_{\theta’}(\Lambda)\approx \sum_{k=0}^K \theta_k’T_k(\tilde{\Lambda}) \end{equation}

$\tilde{\Lambda}$: rescaled as $\frac{2}{\lambda_{max}}\Lambda - I$
$\lambda_{max}$: the largest eigenvalue of $L$
$\theta’ \in \Re^K$: a vector of Chebyshev coefficients.
Chebyshev polynomials: $T_k(x) = 2xT_{k-1}(x)-T_{k-2}(x)$, with $T_0(x) = 1, T_1(x) = 0$

Hence for the definition of convolution: \begin{equation} g_{\theta’}\star x \approx \sum_{k=0}^K \theta_k’T_k(\tilde{L})x \end{equation} where $\tilde{L} = \frac{2}{\lambda_{max}}L - I$, while Eq. (5) is K-localized, which only depends on nodes that are at maximum $K$ steps away from the central node ($K$th-order neighborhood), with the linear time complexity of $\mathcal{O}(|\varepsilon|)$.

Layer-wise linear model

Therefore, a neural network model based on graph convolution can be built by stacking multiple convolution layers of the form of Eq. (5), each layer followed by a point-wise non-linearity. Let $K=1$, it becomes a linear function on the graph Laplacian spectrum. Intuitively, it is expected that such a model can alleviate the problem of overfitting on local neighborhood structures for graph with very wide node degree distributions. In this formulation of a GCN, assume that $\lambda_{max} \approx 2$ and expect the neural network parameters will adapt this change in scale during training. Thus Eq. (5) can be simplified as: \begin{equation} g_{\theta’}\star x \approx \theta_0’x+ \theta_1’(L-I)x = \theta_0’x - \theta_1’D^{-\frac{1}{2}}AD^{-\frac{1}{2}}x \end{equation} In practice, the number of parameters are constrained to address overfitting and to minimize the number of operations per layer: \begin{equation} g_{\theta’}\star x \approx \theta(I+ D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x \end{equation}

$\theta = \theta_0’ = -\theta_1’$
$I+ D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$: has eigenvalues in a range [0,2].

Repeated application of this operator can therefore lead to numerical instabilities and exploding/vanishing gradients when used in a deep neural network model.

Solution by a renormalization trick:

\begin{equation*} I+ D^{-\frac{1}{2}}AD^{-\frac{1}{2}} \rightarrow \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}, \end{equation*} where $\tilde{A} = A + I$, $\tilde{D}_{i,i} = \sum_j\tilde{A}_{i,j}$

Generalize this difinition to signal $X \in \Re^{N\times C}$ with $C$-dimensional feature (input channels) and $F$ filters as: \begin{equation} Z = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}X\Theta \end{equation}

$\Theta \in \Re^{C\times F}$: a matrix of filter parameters
$Z \in \Re^{N\times F}$: the convolved signal matrix
Time complexity: $\mathcal{O}(\epsilon)$, $\tilde{A}X$ can be calculated by a product of a sparse matrix with a dense matrix.

A multi-layer GCN for semi-supervised learning can be depicted as below. GCN

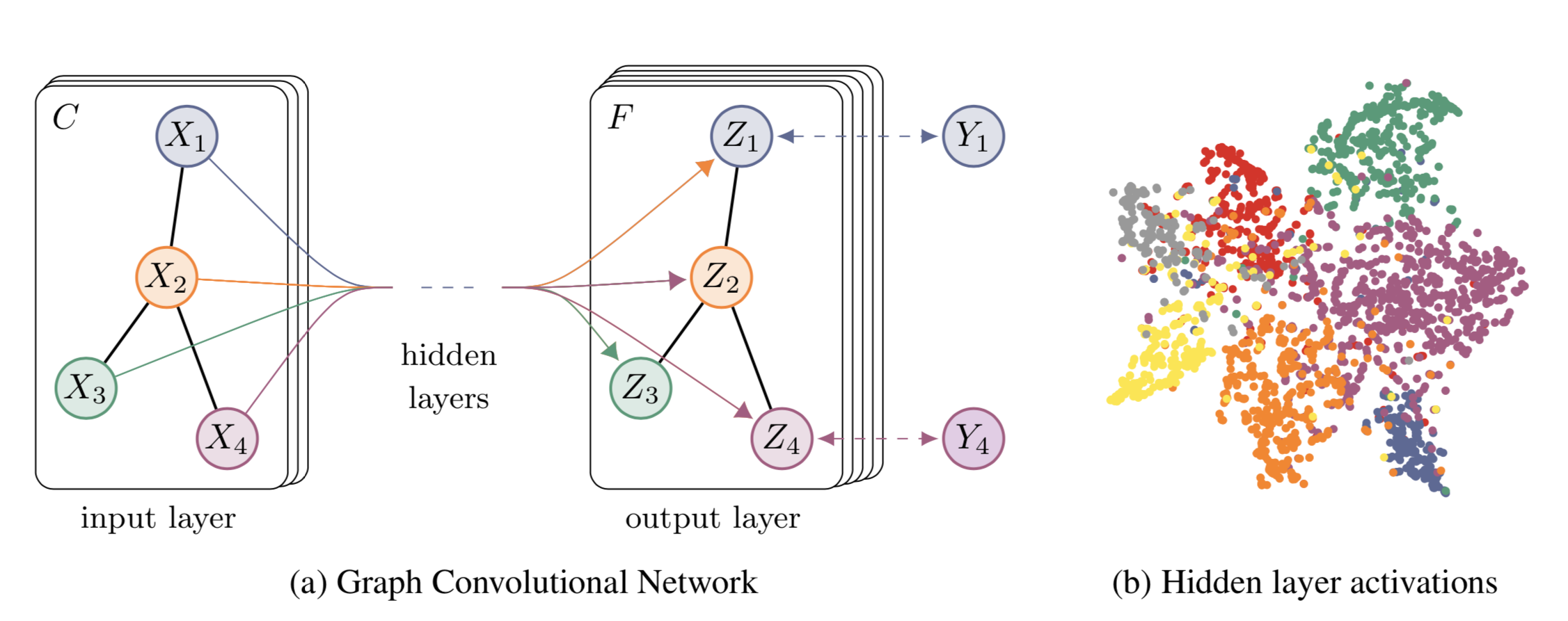
Here gives a two-layer GCN for semi-supervised node classification on a symmetric adjacency matrix A. After pre-calculate $\hat{A} = \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}$, the forward model can be formed as: \begin{equation} Z = f(X,A) = {\rm softmax}(\hat{A}\ {\rm ReLU}(\hat{A}\ XW^{(0)})W^{(1)}) \end{equation}

$W^{(0)} \in \Re^{C\times H}$ is an input-to-hidden weight matrix for a hidden layer with $H$ feature maps.
$W^{(1)} \in \Re^{H\times F}$ is an hidden-to-output weight matrix.
Activation function: ${\rm softmax}(x_i) = \frac{exp(x_i)}{\sum_{i}exp(x_i)}$ is applied row-wise.
Cross-entropy error: \begin{equation} \mathcal{L} = -\sum_{l \in y_L}\sum_{f=1}^{F}Y_{l,f}\ {\rm ln}Z_{l,f} \end{equation} $y_L$ is the set of node indices that have labels.

Neural Networks on Graph

Two categories of graph representation:

models that use some form of explicit graph Laplacian regularization
models that use graph embedding-based approaches

This GCN model uses a single weight matrix per layer and deals with varying node degrees through and appropriate normalization of the adjacency

Code for experiment

Here I use PyTorch Geometric (PyG) [3] to reproduce the experiment on Cora dataset.

import os.path as osp

import torch
import torch.nn.functional as F
from torch_geometric.datasets import Planetoid
import torch_geometric.transforms as T
import numpy as np
from torch_geometric.nn import GCNConv, ChebConv  # noqa

seed = 123
def setup_seed(seed):
    torch.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    np.random.seed(seed)
    torch.backends.cudnn.deterministic = True
setup_seed(seed)
           
# dataset = 'Cora'
# path = osp.join(osp.dirname(osp.realpath(__file__)), '..', 'data', dataset)
# dataset = Planetoid(path, dataset, T.NormalizeFeatures())
dataset = Planetoid(root='/tmp/Cora', name='Cora',pre_transform = T.TargetIndegree())
data = dataset[0]


class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = GCNConv(dataset.num_features, 16, cached=True)
        self.conv2 = GCNConv(16, dataset.num_classes, cached=True)
        # self.conv1 = ChebConv(data.num_features, 16, K=2)
        # self.conv2 = ChebConv(16, data.num_features, K=2)

    def forward(self,data):
        x, edge_index = data.x, data.edge_index
        x = F.relu(self.conv1(x, edge_index))
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)
        return F.log_softmax(x, dim=1)
    

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)


def train(data):
    model.train()
    optimizer.zero_grad()
    out = model(data)
    accs = []
    for _, mask in data('train_mask', 'val_mask'):
        pred = out[mask].max(1)[1]
        acc = pred.eq(data.y[mask]).sum().item() / mask.sum().item()
        accs.append(acc)
    F.nll_loss(out[data.train_mask], data.y[data.train_mask]).backward()
    optimizer.step()
    return accs

def test(data):
    model.eval()
    pred = model(data).max(dim=1)[1]
    correct = pred[data.test_mask].eq(data.y[data.test_mask]).sum().item()
    acc = correct / data.test_mask.sum().item()
    return acc

for epoch in range(1, 201):
    train_acc, val_acc = train(data)
    log = 'Epoch: {:03d}, Train: {:.4f}, Val: {:.4f}'
    print(log.format(epoch, train_acc, val_acc))

test_acc = test(data)
log = 'Test Accuracy : {:.4f}'
print(log.format(test_acc))

Epoch: 001, Train: 0.1643, Val: 0.0620
Epoch: 002, Train: 0.3786, Val: 0.1980
Epoch: 003, Train: 0.5929, Val: 0.3100
Epoch: 004, Train: 0.7429, Val: 0.3880
Epoch: 005, Train: 0.7857, Val: 0.4080
Epoch: 006, Train: 0.8214, Val: 0.4620
Epoch: 007, Train: 0.8429, Val: 0.5000
Epoch: 008, Train: 0.8571, Val: 0.5520
Epoch: 009, Train: 0.8714, Val: 0.5360
Epoch: 010, Train: 0.8714, Val: 0.5700
Epoch: 011, Train: 0.9071, Val: 0.6100
Epoch: 012, Train: 0.9214, Val: 0.5960
Epoch: 013, Train: 0.9500, Val: 0.6580
Epoch: 014, Train: 0.9714, Val: 0.6680
Epoch: 015, Train: 0.9571, Val: 0.6760
Epoch: 016, Train: 0.9357, Val: 0.6780
Epoch: 017, Train: 0.9571, Val: 0.6800
Epoch: 018, Train: 0.9571, Val: 0.6800
Epoch: 019, Train: 0.9714, Val: 0.6800
Epoch: 020, Train: 0.9929, Val: 0.6940
Epoch: 021, Train: 0.9786, Val: 0.7140
Epoch: 022, Train: 0.9714, Val: 0.7000
Epoch: 023, Train: 0.9786, Val: 0.7160
Epoch: 024, Train: 0.9857, Val: 0.6800
Epoch: 025, Train: 0.9786, Val: 0.6860
Epoch: 026, Train: 0.9786, Val: 0.6840
Epoch: 027, Train: 0.9929, Val: 0.6820
Epoch: 028, Train: 0.9929, Val: 0.7120
Epoch: 029, Train: 0.9643, Val: 0.7080
Epoch: 030, Train: 0.9857, Val: 0.6960
Epoch: 031, Train: 0.9857, Val: 0.7460
Epoch: 032, Train: 0.9857, Val: 0.7220
Epoch: 033, Train: 0.9929, Val: 0.6980
Epoch: 034, Train: 0.9786, Val: 0.7160
Epoch: 035, Train: 1.0000, Val: 0.7260
Epoch: 036, Train: 1.0000, Val: 0.7020
Epoch: 037, Train: 1.0000, Val: 0.7460
Epoch: 038, Train: 1.0000, Val: 0.7380
Epoch: 039, Train: 1.0000, Val: 0.7240
Epoch: 040, Train: 0.9857, Val: 0.7240
Epoch: 041, Train: 1.0000, Val: 0.7060
Epoch: 042, Train: 0.9857, Val: 0.7460
Epoch: 043, Train: 1.0000, Val: 0.7280
Epoch: 044, Train: 1.0000, Val: 0.7020
Epoch: 045, Train: 0.9929, Val: 0.7040
Epoch: 046, Train: 1.0000, Val: 0.7240
Epoch: 047, Train: 1.0000, Val: 0.7080
Epoch: 048, Train: 0.9857, Val: 0.7380
Epoch: 049, Train: 0.9857, Val: 0.7120
Epoch: 050, Train: 0.9929, Val: 0.7400
Epoch: 051, Train: 1.0000, Val: 0.7160
Epoch: 052, Train: 1.0000, Val: 0.7240
Epoch: 053, Train: 1.0000, Val: 0.7460
Epoch: 054, Train: 1.0000, Val: 0.7320
Epoch: 055, Train: 0.9857, Val: 0.7160
Epoch: 056, Train: 0.9929, Val: 0.7160
Epoch: 057, Train: 1.0000, Val: 0.7320
Epoch: 058, Train: 1.0000, Val: 0.7380
Epoch: 059, Train: 1.0000, Val: 0.7160
Epoch: 060, Train: 1.0000, Val: 0.7420
Epoch: 061, Train: 1.0000, Val: 0.7060
Epoch: 062, Train: 1.0000, Val: 0.7260
Epoch: 063, Train: 1.0000, Val: 0.7180
Epoch: 064, Train: 0.9857, Val: 0.7500
Epoch: 065, Train: 1.0000, Val: 0.7340
Epoch: 066, Train: 1.0000, Val: 0.7240
Epoch: 067, Train: 1.0000, Val: 0.7240
Epoch: 068, Train: 0.9929, Val: 0.7180
Epoch: 069, Train: 1.0000, Val: 0.7420
Epoch: 070, Train: 0.9857, Val: 0.7380
Epoch: 071, Train: 0.9929, Val: 0.7200
Epoch: 072, Train: 1.0000, Val: 0.7260
Epoch: 073, Train: 1.0000, Val: 0.7260
Epoch: 074, Train: 1.0000, Val: 0.7380
Epoch: 075, Train: 0.9786, Val: 0.7500
Epoch: 076, Train: 0.9929, Val: 0.7340
Epoch: 077, Train: 1.0000, Val: 0.7160
Epoch: 078, Train: 0.9929, Val: 0.7340
Epoch: 079, Train: 0.9929, Val: 0.7300
Epoch: 080, Train: 0.9929, Val: 0.7300
Epoch: 081, Train: 1.0000, Val: 0.7420
Epoch: 082, Train: 1.0000, Val: 0.7640
Epoch: 083, Train: 1.0000, Val: 0.7460
Epoch: 084, Train: 1.0000, Val: 0.7500
Epoch: 085, Train: 1.0000, Val: 0.7460
Epoch: 086, Train: 1.0000, Val: 0.7340
Epoch: 087, Train: 1.0000, Val: 0.7340
Epoch: 088, Train: 0.9929, Val: 0.7400
Epoch: 089, Train: 1.0000, Val: 0.7460
Epoch: 090, Train: 0.9929, Val: 0.7400
Epoch: 091, Train: 0.9929, Val: 0.7400
Epoch: 092, Train: 0.9929, Val: 0.7420
Epoch: 093, Train: 1.0000, Val: 0.7300
Epoch: 094, Train: 1.0000, Val: 0.7340
Epoch: 095, Train: 0.9929, Val: 0.7520
Epoch: 096, Train: 1.0000, Val: 0.7620
Epoch: 097, Train: 0.9857, Val: 0.7160
Epoch: 098, Train: 1.0000, Val: 0.7580
Epoch: 099, Train: 1.0000, Val: 0.7400
Epoch: 100, Train: 1.0000, Val: 0.7520
Epoch: 101, Train: 1.0000, Val: 0.7620
Epoch: 102, Train: 1.0000, Val: 0.7380
Epoch: 103, Train: 1.0000, Val: 0.7200
Epoch: 104, Train: 1.0000, Val: 0.7260
Epoch: 105, Train: 0.9929, Val: 0.7480
Epoch: 106, Train: 1.0000, Val: 0.7240
Epoch: 107, Train: 1.0000, Val: 0.7280
Epoch: 108, Train: 1.0000, Val: 0.7520
Epoch: 109, Train: 1.0000, Val: 0.7420
Epoch: 110, Train: 1.0000, Val: 0.7320
Epoch: 111, Train: 1.0000, Val: 0.7320
Epoch: 112, Train: 1.0000, Val: 0.7280
Epoch: 113, Train: 1.0000, Val: 0.7540
Epoch: 114, Train: 0.9929, Val: 0.7800
Epoch: 115, Train: 1.0000, Val: 0.7160
Epoch: 116, Train: 1.0000, Val: 0.7420
Epoch: 117, Train: 0.9929, Val: 0.7300
Epoch: 118, Train: 1.0000, Val: 0.7260
Epoch: 119, Train: 1.0000, Val: 0.7380
Epoch: 120, Train: 1.0000, Val: 0.7420
Epoch: 121, Train: 1.0000, Val: 0.7240
Epoch: 122, Train: 1.0000, Val: 0.7140
Epoch: 123, Train: 1.0000, Val: 0.7260
Epoch: 124, Train: 1.0000, Val: 0.7640
Epoch: 125, Train: 0.9929, Val: 0.7600
Epoch: 126, Train: 1.0000, Val: 0.7080
Epoch: 127, Train: 1.0000, Val: 0.7420
Epoch: 128, Train: 0.9929, Val: 0.7460
Epoch: 129, Train: 0.9929, Val: 0.7240
Epoch: 130, Train: 1.0000, Val: 0.7400
Epoch: 131, Train: 0.9929, Val: 0.7340
Epoch: 132, Train: 0.9929, Val: 0.7020
Epoch: 133, Train: 1.0000, Val: 0.7140
Epoch: 134, Train: 1.0000, Val: 0.7480
Epoch: 135, Train: 1.0000, Val: 0.7260
Epoch: 136, Train: 1.0000, Val: 0.7460
Epoch: 137, Train: 0.9857, Val: 0.7280
Epoch: 138, Train: 0.9929, Val: 0.7300
Epoch: 139, Train: 1.0000, Val: 0.7300
Epoch: 140, Train: 1.0000, Val: 0.7480
Epoch: 141, Train: 1.0000, Val: 0.7500
Epoch: 142, Train: 0.9929, Val: 0.7360
Epoch: 143, Train: 1.0000, Val: 0.7240
Epoch: 144, Train: 1.0000, Val: 0.7380
Epoch: 145, Train: 1.0000, Val: 0.7380
Epoch: 146, Train: 0.9929, Val: 0.7380
Epoch: 147, Train: 0.9929, Val: 0.7480
Epoch: 148, Train: 1.0000, Val: 0.7280
Epoch: 149, Train: 1.0000, Val: 0.7520
Epoch: 150, Train: 1.0000, Val: 0.7180
Epoch: 151, Train: 1.0000, Val: 0.7460
Epoch: 152, Train: 1.0000, Val: 0.7380
Epoch: 153, Train: 1.0000, Val: 0.7160
Epoch: 154, Train: 1.0000, Val: 0.7360
Epoch: 155, Train: 1.0000, Val: 0.7420
Epoch: 156, Train: 1.0000, Val: 0.7260
Epoch: 157, Train: 1.0000, Val: 0.7180
Epoch: 158, Train: 0.9929, Val: 0.7420
Epoch: 159, Train: 1.0000, Val: 0.7240
Epoch: 160, Train: 0.9929, Val: 0.7440
Epoch: 161, Train: 1.0000, Val: 0.7260
Epoch: 162, Train: 0.9857, Val: 0.7220
Epoch: 163, Train: 1.0000, Val: 0.7200
Epoch: 164, Train: 1.0000, Val: 0.7180
Epoch: 165, Train: 1.0000, Val: 0.7360
Epoch: 166, Train: 0.9929, Val: 0.7340
Epoch: 167, Train: 1.0000, Val: 0.7360
Epoch: 168, Train: 1.0000, Val: 0.7560
Epoch: 169, Train: 1.0000, Val: 0.7440
Epoch: 170, Train: 1.0000, Val: 0.7380
Epoch: 171, Train: 1.0000, Val: 0.7280
Epoch: 172, Train: 1.0000, Val: 0.7480
Epoch: 173, Train: 0.9857, Val: 0.7320
Epoch: 174, Train: 1.0000, Val: 0.7500
Epoch: 175, Train: 1.0000, Val: 0.7080
Epoch: 176, Train: 1.0000, Val: 0.7320
Epoch: 177, Train: 0.9929, Val: 0.7540
Epoch: 178, Train: 1.0000, Val: 0.7320
Epoch: 179, Train: 1.0000, Val: 0.7340
Epoch: 180, Train: 1.0000, Val: 0.7220
Epoch: 181, Train: 1.0000, Val: 0.7200
Epoch: 182, Train: 1.0000, Val: 0.7340
Epoch: 183, Train: 1.0000, Val: 0.7440
Epoch: 184, Train: 1.0000, Val: 0.7420
Epoch: 185, Train: 1.0000, Val: 0.7360
Epoch: 186, Train: 1.0000, Val: 0.7300
Epoch: 187, Train: 0.9929, Val: 0.7460
Epoch: 188, Train: 1.0000, Val: 0.7380
Epoch: 189, Train: 1.0000, Val: 0.7180
Epoch: 190, Train: 0.9929, Val: 0.7400
Epoch: 191, Train: 1.0000, Val: 0.7580
Epoch: 192, Train: 1.0000, Val: 0.7340
Epoch: 193, Train: 1.0000, Val: 0.7320
Epoch: 194, Train: 1.0000, Val: 0.7400
Epoch: 195, Train: 0.9857, Val: 0.7480
Epoch: 196, Train: 0.9929, Val: 0.7300
Epoch: 197, Train: 1.0000, Val: 0.7320
Epoch: 198, Train: 1.0000, Val: 0.7520
Epoch: 199, Train: 1.0000, Val: 0.7420
Epoch: 200, Train: 1.0000, Val: 0.7440
Test Accuracy : 0.8090

The result is same as the test accuracy (0.809) of the example code from Kipf.

References

[1] Kipf, T.N. and Welling, M., 2016. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907.

[2] David K. Hammond, Pierre Vandergheynst, and Re ́mi Gribonval. Wavelets on graphs via spectral graph theory. Applied and Computational Harmonic Analysis, 30(2):129–150, 2011.

[3] Fey, M. and Lenssen, J.E., 2019. Fast Graph Representation Learning with PyTorch Geometric. arXiv preprint arXiv:1903.02428.

Semi-Supervised Classification with Graph Convolutional Networks

Literuture Review