https://arxiv.org/abs/1605.05273
Idea
归一化的拉普拉斯矩阵:$L=I_N - D^{-\frac{1}{2}}AD^{-\frac{1}{2}} = U\Lambda U^T$
傅立叶卷积: $g_\theta\star x = Ug_\theta U^Tx$.
Graph Convolutionn Networks 用截断的切比雪夫多项式近似: $g_{\theta}(\Lambda)\approx \sum_{k=0}^K \theta_kT_k(\Lambda)$,得到k-localized kernel for k-hop vertices.
两个结点之间的相似度是由所采取的距离度量和特征域决定的,存在一种可能:两个连接节点的相似性有可能低于两个没有连接的节点(due to raw feature and/or intrinsic graph topology),因此图结构不是最优的
AGCN 参数化拉普拉斯矩阵而不是$\theta_k$: $g_{\theta}(\Lambda)\approx \sum_{k=0}^K (\mathcal{F}(L,X,\Gamma))^k$, 同样用切比雪夫展开式近似。
计算复杂度$\mathcal{O}(N^2)$ due to dense matrix multiplication,N个训练样本独有的图拓扑结构需要学习N个独有的图Laplacian。
Solution:利用Mahalanobis距离作为一个监督度量学习,假定度量的参数是样本之间共享的。\begin{equation} \mathbb{D}(x_i,x_j) = \sqrt{(x_i-x_j)^TM(x_i,x_j)} \end{equation} $M = W_d^TW_d$,$W_d \in \mathbb{R}^{d\times d}$ 是可训练的参数。
用这个距离计算高斯核: \begin{equation} \mathbb{G}_{x_i,x_j} = \rm{exp}(-\mathbb{D}(x_i,x_j)/(2\sigma^2)) \end{equation} 归一化$\mathbb{G}$,得到dense邻接矩阵。在模型中,最优度量能够建立最优的图Laplacian集,使得预测损失最小化。
此外并提出重参数化,在特征域上加个转换权重和偏置:$Y = (Ug_\theta(\Lambda)U^TX)W+b$.
由于对距离度量没有先验知识,所以$M$被随机初始化,这会导致收敛速度变慢。 所以提出一个假设:最初的L已经包括了大量的有用图结构信息,但不包括那些由虚拟结点连接组成的子结构,这些虚拟结点连接不能直接从固有图中学习到,所以残差图可以用于探索固有图中没有包括的剩余子结构,并更新L。
\begin{equation} L_{res}(i) = \mathcal{L}(M_i,X), \hat{L} = L + \alpha L_{res} \end{equation}
pseudo-code
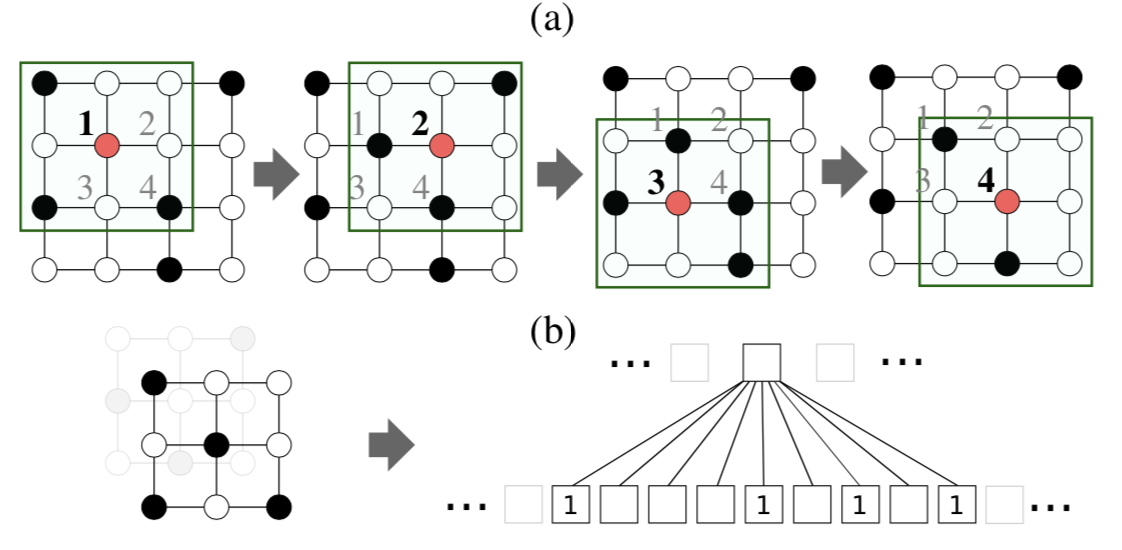
Reference
[1] Niepert, M., Ahmed, M. and Kutzkov, K., 2016, June. Learning convolutional neural networks for graphs. In International conference on machine learning (pp. 2014-2023).