https://arxiv.org/abs/1605.05273
Introduction
This paper is proposed by Niepert, Mathias, Mohamed Ahmed, and Konstantin Kutzkov in 2016 on ICML.
This blog will review the paper and reproduce some experiments. [code]
It proposed a framework for learning convolution neural network for arbitrary graphs, which can be directed, undirected and with both discrete and continuous node and edge attributes.
Analogous to image-based CNNs which operate on locally connected regions of the input, this paper proposed a approah to extract locally connected resion from graphs.
problem
- nodes for any two graphs are not necessarily in correspondence.
- how to learn graph representations to infer unseen graph properties (node types / missing edges)
Convolutional on Graph
** This can be seen as traversing in a node sequence and generating fixed-size neighborhood graph.**
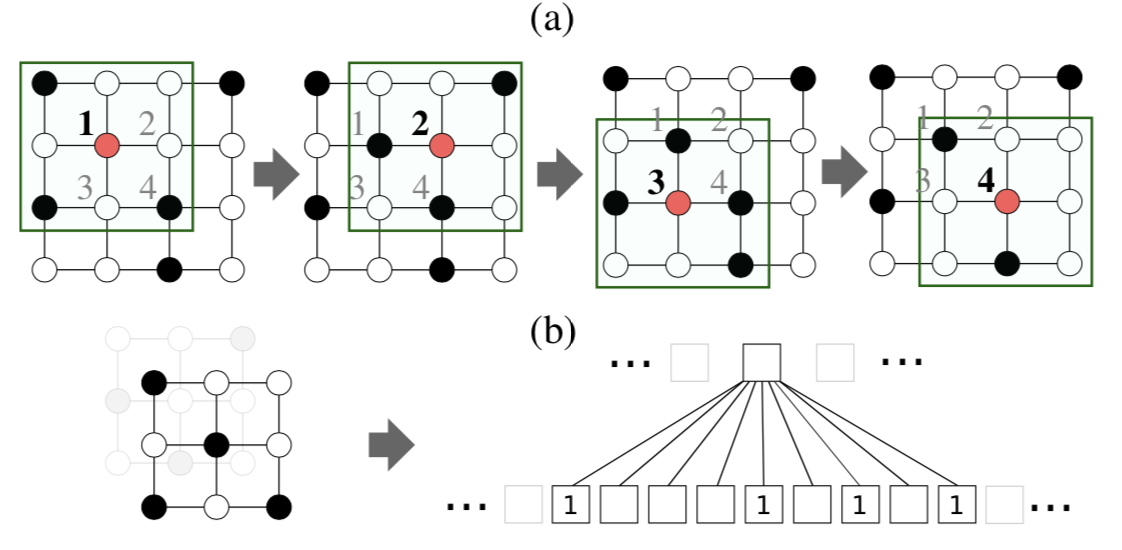
To sovle two prolems by PATCHY-SAN
-
Determining the node sequences for which neighborhood graphs are created. (by hyperparameter)
-
Computing a normalization of neighborhood graphsa unique map- ping from a graph representation into a vector space representation.
Process:
- Determine nodes and order;
- Create neighborhood graphs;
- Extract and normalize the neighborhood, which serves as the receptive field for a node under consideration.
Advantages:
- high efficient, naively paralleizable and applicable to large graphs;
- support feature visualizations;
- can learning application dependent features without feature engineering.
Proposed Method
The architecture of this algorithm can be seen:
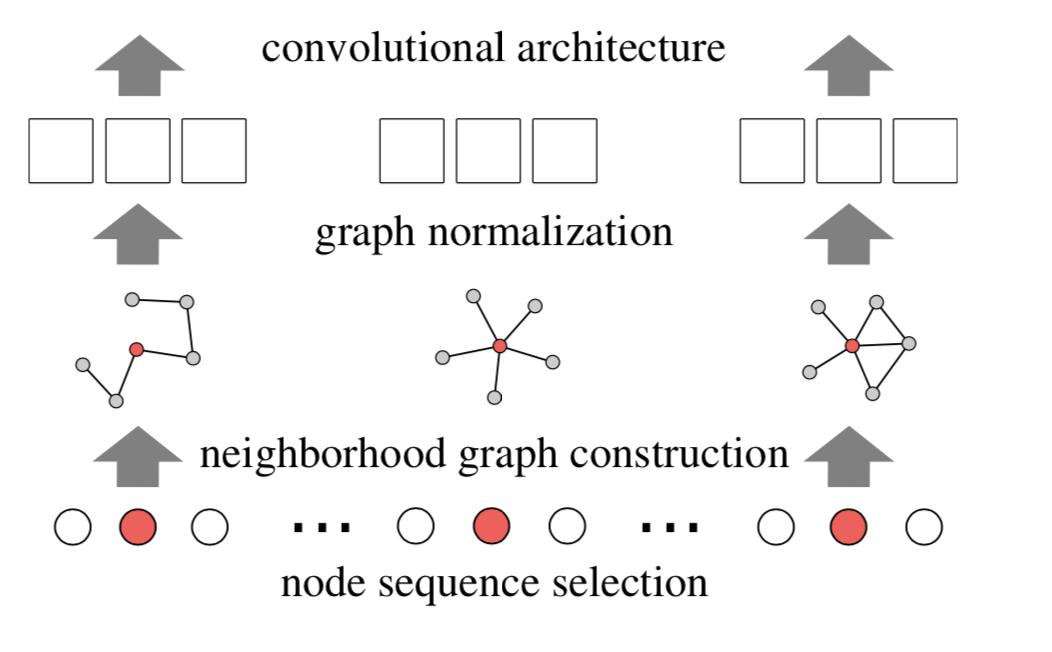
Node Sequence Selection
Select a fixed-length sequence of nodes from the graph
Graph Labeling, $e.g.$ betweeness centrality, Weisfeiler-Lehman, to get a structured sequence like imposing an order on the nodes of graph or Rank.
Procedure:
- Sorted by graph labeling;
- Traverse the node sequence to construct receptive fields for each input channel.
Neighborhood Assembly
Assemble a fixed-size neighborhood for each node in the selected sequence
- Given as inputs a node $v$ and the size of the receptive field $k$
- Performs a breadth-first search to expore vertices with an increase distance from $v$
- add these vertices to a set $N$, $i.e.$ neighborhood.
- (make sure at least $k$ vertives are in $N$, or no more neighbors to add)
Graph Normalization
Normalize the extracted neighborhood graph
The receptive field for a node is constructed by normalizing the neighborhood assembled in the previous step.
The normalization imposes an order on the nodes of the neighborhood graph so as to map from the unordered graph space to a vector space with a linear order.

Convolutional Architecture
Learn neighborhood representations with convolutional neural networks from the resulting sequence of patches.
Reference
[1] Niepert, M., Ahmed, M. and Kutzkov, K., 2016, June. Learning convolutional neural networks for graphs. In International conference on machine learning (pp. 2014-2023).